Всички ние знаем как да си вземем топъл шоколад от близката кафе-машина. Процесът преминава през следните стъпки: пускаме монета, после избираме напитка и количество захар, изчакваме звуковия сигнал и вземаме напитката си. Всички указания, изпълнени в посочената последователност, представляват алгоритъм за получаване на напитка от кафе-машината. Този алгоритъм се състои от последователни действия (стъпки).
АЛГОРИТЪМ
Алгоритъм наричаме крайна последователност от действия над определени входни данни, която задава стъпките и реда на тяхното изпълнение с цел постигане на резултат от решаването на определена задача.

Защо е важен алгоритъмът на Instagram или на Google?
ЛЮБОПИТНО
Абу Джафар Мохамед ибн Муса ал-Хорезми е арабски учен от IX век. Роден е около 780 г. в околностите на град Хорезъм (дн. Туркменистан). Той е енциклопедичен учен – математик, физик, историк, астроном, но до нас е достигнал като „баща на алгебрата“. Написал е много книги в различни области на науката. Един латински превод на негова книга започва с думите: „Dixit Algorizmi“ („Така казва Ал-Хорезми“). Постепенно преиначеното име „алгоризми“ станало познатото ни „алгоритъм“.
Задача 18
Разгледайте следните примери за алгоритми за математически изчисления:
Пример 1: Алгоритъм за намиране на лице на триъгълник по дадена страна и височина към нея: Входни данни: a и h, a>0, h>0: Резултат: S – лице на триъгълник
Стъпка 1. Задава се стойност на страната а.
Стъпка 2. Задава се стойност на височината h.
Стъпка 3. Изчислява се S = a*h/2.
Стъпка 4. Извежда се лицето S.
Стъпка 5. Край.
Пример 2: Алгоритъм за решаване на линейно уравнение a.x + b = 0:
Входни данни: a, b
Резултат: решението на уравнението или съобщение за липсата на такова
Стъпка 1. Ако а = 0, се преминава към стъпка 2, в противен случай се извежда единственото решение на уравнението x = – b/a.
Стъпка 2. Ако b = 0, се извежда съобщение „Всяко х е решение на уравнението“. В противен случай се извежда съобщение „Уравнението няма решения“ и се преминава към стъпка 3.
Стъпка 3. Край.
Пример 3: Алгоритъм на Евклид за намиране НОД на две естествени числа p и q.
Входни данни: p и q – естествени числа: Резултат: НОД(p, q)
Стъпка 1. Делим p на q с частно и остатък. Означаваме r = остатъка от p/q.
Стъпка 2. Ако r = 0, то НОД = q. Отпечатваме резултата и преминаваме към стъпка 3. В противен случай правим замяна: p = q; q = r, и преминаваме към стъпка 1.
Стъпка 3. Край.
Свойства на алгоритмите
Основни свойства на алгоритмите са:
● дискретност – всеки алгоритъм трябва да се състои от отделни, разграничени една от друга стъпки, всяка от които се извършва за крайно време;
● детерминираност – резултатът от действията върху данните и посочването на следващата стъпка трябва да бъде еднозначно определен от действията, извършвани в текущия момент;
● определеност – при едни и същи данни се получава един и същи резултат;
● масовост – всеки алгоритъм трябва да се използва успешно при решаване на много проблеми от този вид, не само за един случай;
● крайност – всеки алгоритъм трябва да завърши с резултат след краен брой стъпки;
● резултатност – всеки алгоритъм трябва винаги да дава резултат, ако входните данни принадлежат на допустимото множество;
● формалност – изпълнителят на алгоритъма изпълнява формално указанията, докато стигне до указание за край. Това свойство позволява изпълнителят на алгоритъма да е някакво механично устройство.
Видове алгоритми
Според последователността на изпълнение на действията алгоритмите се делят на различни видове.
Линеен алгоритъм, в които действията се изпълняват последователно по реда, в който са записани.
Алгоритъмът от Пример 1 е линеен.

Посочете примери за линеен алгоритъм от всекидневието си.
Често в практиката се налага да се вземе решение и да се изпълни едно или друго действие. Такива ситуации се описват чрез разклонени алгоритми. Разклонението дава възможност да се избере един от вариантите за продължаване на изчислителния процес.
Алгоритъм, чието изпълнение се разделя на различни последователности от действия в зависимост от верността на дадено условие, се нарича разклонен.
Алгоритъмът от Пример 2 е разклонен. В зависимост от стойността на коефициента пред неизвестното изчислителният процес продължава в различни посоки.

За какво ви се налага най-често да вземете решение? Посочете примери за разклонен алгоритъм от всекидневието си.
Алгоритъм, в който дадена група от елементарни действия се изпълнява многократно, се нарича цикличен.
Повтарящите се действия наричаме тяло на цикъла, а всяко изпълнение на тялото на цикъла – итерация. Тъй като според свойството крайност всеки алгоритъм трябва да завърши след определен брой стъпки, е необходимо да се обърне особено внимание на условието за край, което трябва да притежава всеки цикличен алгоритъм. В Пример 3 (с. 21) алгоритъмът е цикличен. Той се изпълнява, докато остатъкът от делението не стане равен на 0. В този случай броят итерации не е известен предварително и зависи от въведените стойности на p и q.
Представяне на алгоритмите
Естествените езици предполагат възможността от неясно и двусмислено изразяване. Това ги прави неподходящи за описание на алгоритмите, при които лаконичното и недвусмислено записване на елементарното действие е задължително (поради свойството детерминираност). Алгоритмите се представят недвусмислено само чрез езиците за програмиране. В следващите уроци ще се научите да представяте алгоритмите на някой от езиците за програмиране Java, C#, JavaScript или Python.
Алгоритмите може да се представят по различни начини:
● текстово описание; псевдокод;
● видео/анимация;
● графично (с блок схеми);
● с език за програмиране.
Задача 1
Отворете папка algo23 и разгледайте различните представяния на един и същ алгоритъм. Кое представяне е най-ясно за вас?
Графично представяне на алгоритми
БЛОК-СХЕМИ
Графичното представяне на алгоритмите чрез т.нар. блок-схеми се използва отдавна в програмирането. Основното му качество е, че позволява по-лесно да се представят графично и да се проследят разклоненията в алгоритъма. Всеки блок определя действие, а когато действието е изпълнено, работата на алгоритъма продължава с блока, до който води излизащата стрелка.

Кое представяне е най-ясно според вас?
Основните блокове са:
1. Блокове за начало и край
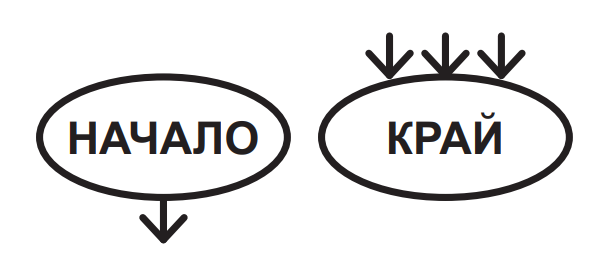
Те са с овална форма. Блокът НАЧАЛО определя мястото, от което започва изпълнението на алгоритъма, и се среща еднократно в блок-схемата. От него излиза само една стрелка, показваща кой е следващият блок. Блокът КРАЙ определя стъпката, в която се прекратява изпълнението на алгоритъма. Във всеки алгоритъм има поне един такъв блок. От него не излиза стрелка, но може да влизат няколко.
2. Блокове за вход и изход
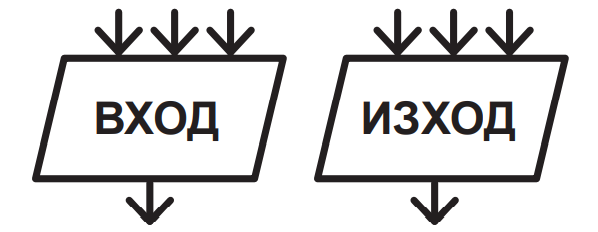
Имат форма на успоредник. В блока за ВХОД се описват входните данни, а блокът за ИЗХОД указва стъпката, при която се извеждат междинните или крайните резултати. Към тези блокове може да сочат няколко стрелки, но излиза само една, която указва следващия блок в алгоритъма.
3. Блок за обработка
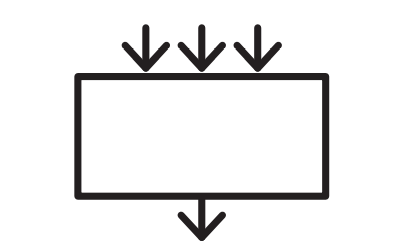
Той има форма на правоъгълник и в него се описват всички операции над обекти, като изчисляване на изрази и запазване на резултатите. Към този блок може да водят няколко стрелки, но излиза само една.
4. Условен блок
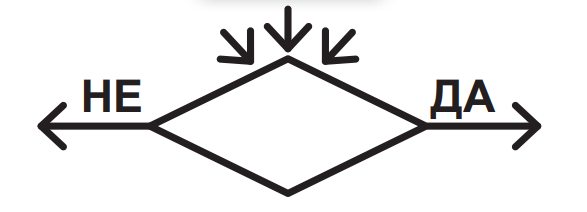
Има форма на ромб. С него се проверява изпълнението на някакво условие. Ако това условие е изпълнено, се преминава към изпълнението на блока, към който сочи стрелката с надпис ДА (true), а ако не – към изпълнението на блока, към който сочи стрелката с надпис НE (false). Към този блок може да сочат няколко стрелки, но излизат само две. Условният блок се използва при описание на разклонени алгоритми.
Нека представим алгоритмите от примерите по-горе чрез блок-схеми. Знакът „=“ има по-различен смисъл от математиката. С него ще означаваме присвояването (задаването) на стойност, а проверката дали едно число е равно на дадена стойност, ще бележим със знака „==“.
Например, за да проверим дали числото a e нула, ще пишем a==0.
Задача 20
Направете блок-схема на проверката дали едно число е четно.
Диаграма от вида „ВХОД – ОБРАБОТКА – ИЗХОД“ – IPO ( Input Processing Output)
Задача 21
Опишете IPO модел на алгоритъм за стопляне на супа с микровълнова печка.
В практиката се използва и диаграмата IPOS (Input, Process, Output, Storage, Feedback). Тя е разширение на диаграмата IPO и включва съхраняване (storage), защото обработката може да е със съхраняване на данни. Използва се, когато данните не се извеждат веднага, а да се запазват за по-дълго време. Последният елемент е за обратна връзка (feedback). Ако има данни, които се съхраняват на диск и са необходими за обработката, то те са вече входни данни за програмата. Когато данните се записват върху диск, те са изход. Обратната връзка (feedback) се използва, когато изходът се връща в системата (автопилоти).